Noir Explained: Features and Examples

Introduction

According to the Developer Report from Electric Capital, in 2023, the Aztec Protocol took the top spot for the growth of full-time developers who are building solutions for the Aztec ecosystem using a specially created Domain-Specific Language (DSL) called Noir.

The goal of this article is to dive into the key features of Noir and understand briefly how it works.

Noir is a Domain-Specific Language for SNARK proving systems developed by Aztec Labs. It allows you to generate complex Zero-Knowledge Programs by using simple and flexible syntax, requiring no previous knowledge on the underlying mathematics or cryptography.

• DSL’s are specialized programming languages designed to solve a specific class of problems. They differ from general-purpose programming languages (like Python, Java, or C++) because they offer abstractions and syntax aimed at a specific application area, making it easier for developers to solve niche tasks more efficiently and accurately. Examples of DSL include Cairo, Leo, Circom, etc. In a way, Solidity and Vyper can also be considered as DSL’s.

Noir is a fresh face in the Zero Knowledge sphere, blending the best industry solutions with a wealth of accumulated experience.

One interesting thing is that Aztec’s core circuits have been rewritten in Noir. They were previously written in C++. The circuits spanning private execution, public execution, and proof recursion are now in Noir.

There are 3 main reasons why the syntax of Noir is very similar to Rust:

1. Headache-free dependency management. Noir has its own package manager, nargo, that mocks Rust’s crate and package management system. nargo supports using dependencies uploaded to Github, allowing devs to separate the dependencies of their Noir circuits and the project integrating those circuits.
2. Simpler circuit debugging. Rather than writing scripts and downloading proving and verifier keys, developers can also use nargo to prove and verify circuits.
3. Autonomous execution. Finally, straight out of the box Noir allows you to build a compiled Solidity contract to verify proofs on any EVM-compatible blockchain. Smart contract developers can now execute logic based on Noir proofs.

What’s even cooler is that Noir can be used to write full-fledged smart contracts on the Aztec Network! This is made possible by using the Aztec.nr framework, which extends Noir with everything developers need to write smart contracts, with Rust-like syntax, seamless state management, and a library of privacy primitives. Aztec.nr allows developers to write private smart contracts and extend their functionality with templated functions that simplify state management.

To understand why Noir is so unique and impressive, we need to:

1. Look into the key features of Noir
2. Dive into the compilation process
3. Show its effectiveness in simple examples.

Noir features

Let’s start by exploring the key features of Noir. We assure you, there’s plenty to see here. Even though Aztec itself is still actively evolving and has been in beta for two years, Noir is already equipped with a minimum required amount of features that you can test in your projects. So, let’s dive into it!

Two-stage compilation

Noir shares a lot with Rust and is built on a two-stage code compilation process:

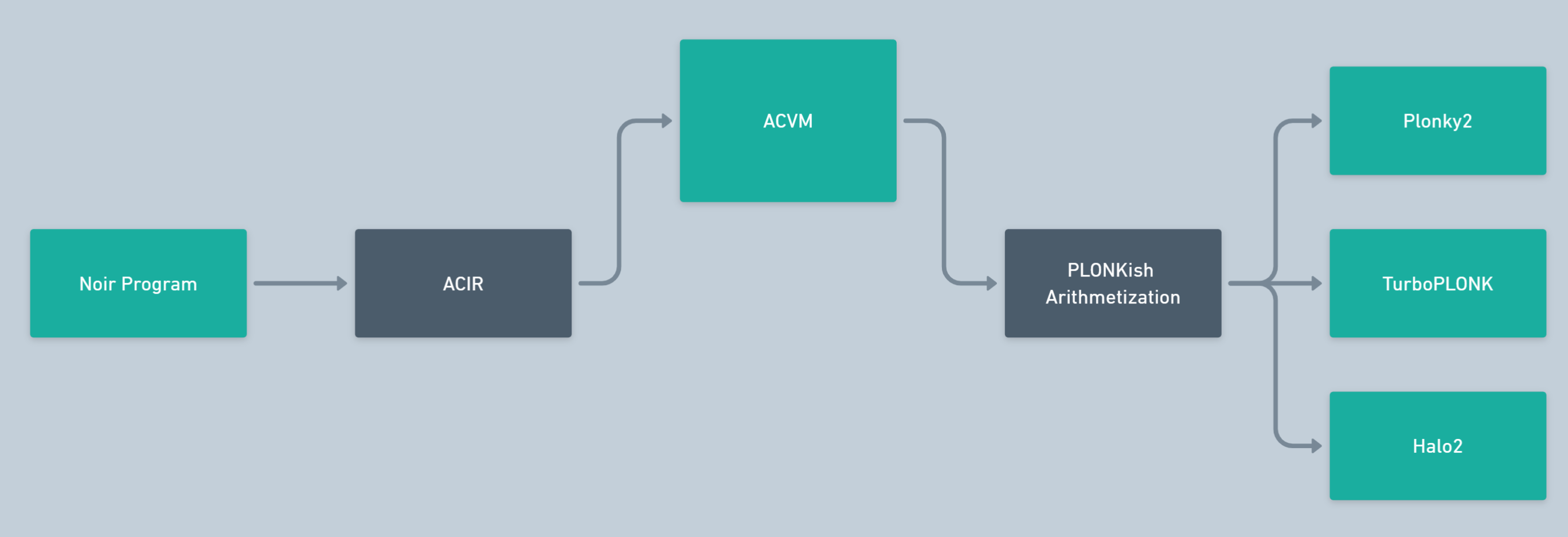
1. From the Noir program itself, a sort of “bytecode” is generated, known as ACIR (Abstract Circuit Intermediate Representation), which is then fed into the ACVM (Abstract Circuit Virtual Machine). This stage is similar to how in Solidity we first compile abstract code into bytecode and then feed it to the EVM, which breaks down the whole bytecode into separate machine instructions (opcodes) and sequentially executes them.
2. ACVM translates the ACIR-bytecode into PLONKish Arithmetization or R1CS, after which an optimized final circuit is generated based on the chosen backend system. At this stage, the virtual machine selects the most optimal PLONKish implementation for the final circuit (for example, it’s quite challenging to integrate circuits directly between R1CS and Arithmetization algorithms, but the optimization offered in Noir greatly simplifies this process by introducing an intermediate stage). This means Noir is a Backend-Agnostic system, allowing for easy work with a multitude of proving systems. Noir already supports TurboPLONK, UltraPLONK, Groth16, Halo2, Plonky2, and other PLONK-like backend systems.

One of the most challenging aspects of, say, Circom, is that developers must independently define and assign all constraints to write a secure program. To manage all necessary constraints often requires a significant amount of knowledge in applied cryptography and mathematics, significantly raising the entry barrier to the field and, consequently, to the mass adoption of ZK solutions. Noir aims to solve this and many other problems of the first DSL’s, making the process of writing arithmetic circuits as straightforward as writing code for smart contracts.

Black Box functions

To overcome the previously mentioned challenge of optimizing constraints when using different backend systems, Noir wraps functions that require substantial computational efforts into separate ACIR opcodes. This means that during the program’s compilation stage, any complex operation performed will be optimized for the target proving system.

For example, if we have a classic KECCAK256 operation, when executed within TurboPLONK, one implementation will be used, while within Halo2, another, more optimized for the peculiarities of the proving system, will be utilized.

This approach significantly reduces the total number of constraints (=decreases the amount of necessary computational efforts🎉).

Currently, Noir supports quite a large number of Black Box Functions, and you can check out its up-to-date list on the language documentation page.

Recursive proofs

Noir also supports working with recursive proving through the use of the #[recursive] attribute. Recursion is the ability of one Noir program to verify the result of another Noir program. Having recursion allows for significantly reducing the size of large ZK proofs. When applied, it informs the compiler and the tooling that the circuit should be compiled in a way that makes its proofs suitable for recursive verification. This attribute eliminates the need for manual flagging of recursion at the tooling level, streamlining the proof generation process for recursive circuits.

Below is an example of a recursive function. This function simply checks the equality of two imports. However, thanks to the relevant attribute, the result of this function can be verified in another Noir program.

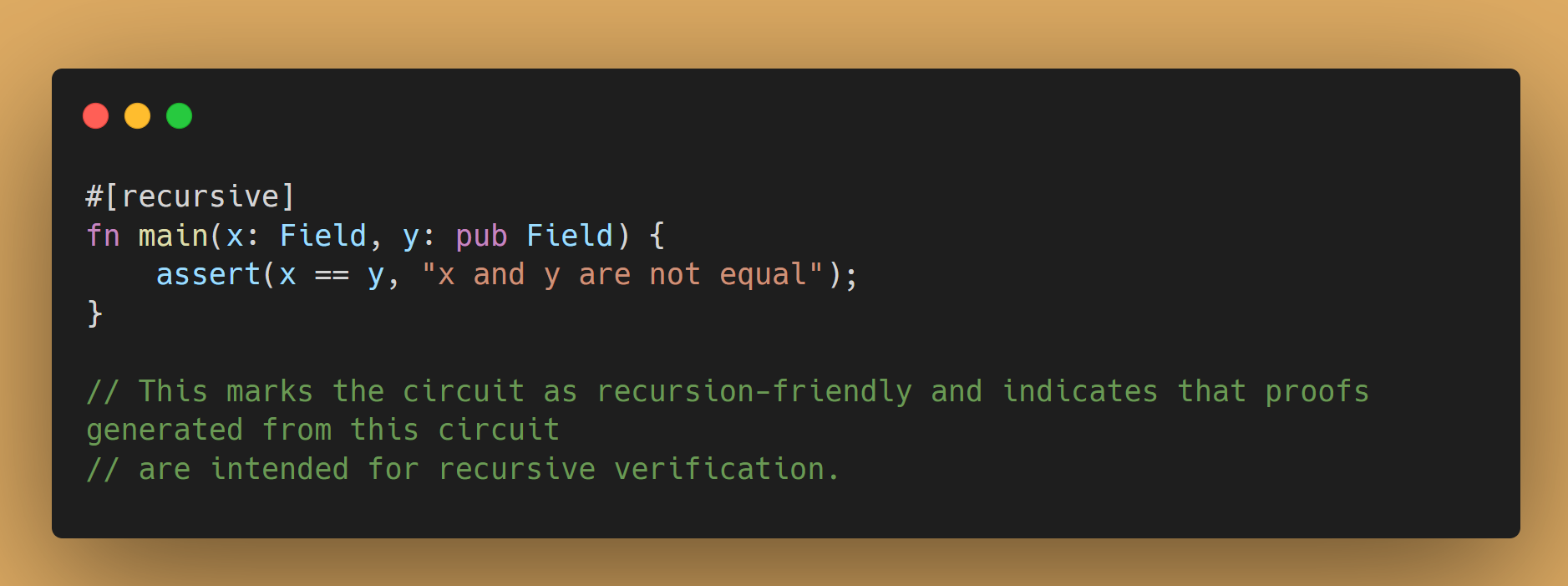
By incorporating this attribute directly into the circuit definition, tools like Nargo and NoirJS can automatically execute recursive functions for Noir programs (for example, recursive-friendly proof artifact generation) without any additional flags or configurations.

Now we understand, how we can generate a ZK Proof using main function. But how can we verify this proof? To do that, we need a separate method. Let’s take a look at an example of a function that allows verifying the result of the program from the previous example.

As you can see, we use a verify_proof function from std lib for that purpose, which is marked as #[foreign()]. It means that function is implemented from external library.

Unconstrained functions

Noir has introduced the use of the unconstrained modifier, which can be useful when a ZK program needs to perform a large number of computations that can be easily verified. The values these functions produce are not translated into constraints and overall do not impact the size and generation time of the final ZK-proof.

In the example below, you can see a function that calculates the square root of an input. The use of the unconstrained modifier here can significantly reduce the number of final constraints:

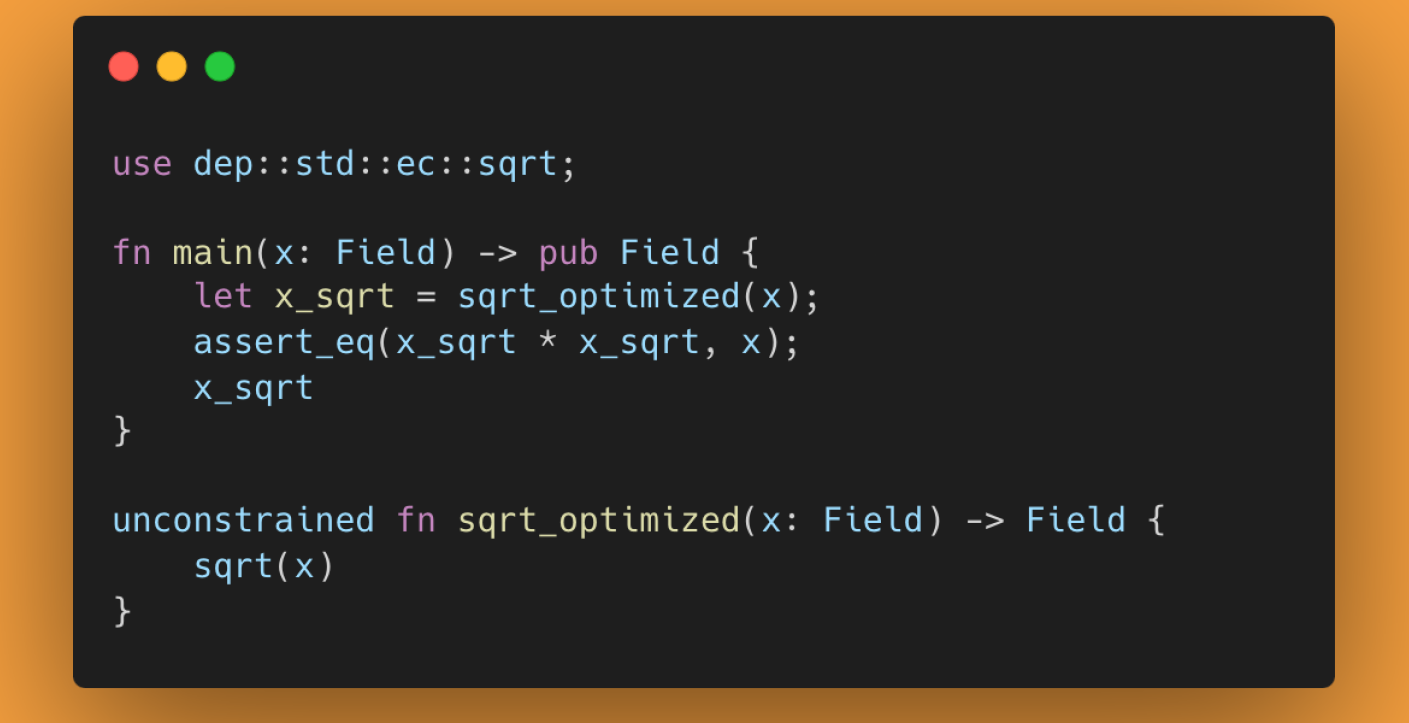
Basic version: 843 constraints Optimized version: 7 constraints!

RPC communication inside the circuit

In programs written in Noir, you can make JSON RPC-requests from the circuit to oracles, allowing the use of the oracle’s return value in the proof generation process.

Oracles can be used to verify on-chain and off-chain information, generate proofs that affirm your ownership rights or authorize you in a system. However, it’s not the oracles themselves that do this – it’s your Noir program. It generates the evidence (proof) that the information provided by the oracle is trustworthy.

If you don’t constrain the return of your oracle, you could be clearly opening an attack vector on your Noir program. Make double-triple sure that the return of an oracle call is constrained!

To handle requests, your system will definitely need an RPC node. For this, you’ll need to write your own server implementation (fortunately, there’s a guide for that). In the vast majority of cases, Aztec.js is used for forming requests, covering all standard interaction scenarios.

Below you can see an example where an oracle returns the result of the sqrt_optimized function. It takes an input x of type Field, and also returns an output of type Field.

Noir Std Lib

Noir boasts a very good standard library that includes many cryptographic primitives such as keccak, sha3, blake2/3. It allows for the integration of Merkle tree membership proofs, ECDSA implementation, and the verify_proof function, which enables adding recursive proving to your program (and much more).

Noir Security Considerations & Problems

However, it’s important to note that Noir also has some security issues that cannot be overlooked.

1. Similar to Circom, in Noir, there are some cases in which your circuits might be underconstrained. For example, if oracle outputs are not properly verified, or if the function was mistakenly marked with #unconstrained attribute. This could lead to unforeseen user behavior and potentially full-scale hacks.
2. As in Circom, Noir has an issue where the Optimizer ignores unused variables, and they do not reflect in the final proof. We discussed the solution to this and other circuit problems in one of our previous articles.
3. As mentioned earlier, special attention should be paid to the validation of values supplied by oracles through RPC-requests. If they are not adequately validated, your program could be vulnerable to serious attacks.
4. It’s important to note that division in Noir works somewhat unconventionally, much like in Cairo - the division process is considered as “multiplication in reverse”. Because of this, using division in Noir can lead to the same vulnerabilities as those found in Cairo during division. You can read more about these vulnerabilities here. However, you can also use a standard division for u64, u128 and some another data types, but be aware using the division of Field data!
5. Noir is still under active development and has not yet been audited! So, be cautious with any financial operations!

Noir by example

Now let’s take a look at examples of basic algorithm implementations in Noir, and compare them with similar implementations in Circom. This comparison will visually demonstrate the differences between these DSLs and the benefits of using Noir.

We will explore the implementation of simple logic for private voting. The first implementation will be in Noir, and the second in Circom.

Let’s start with the Noir implementation. The program below is designed to implement private voting using Zero-Knowledge Proofs. This technology allows users to prove that their votes meet all the election requirements without disclosing any personal information:

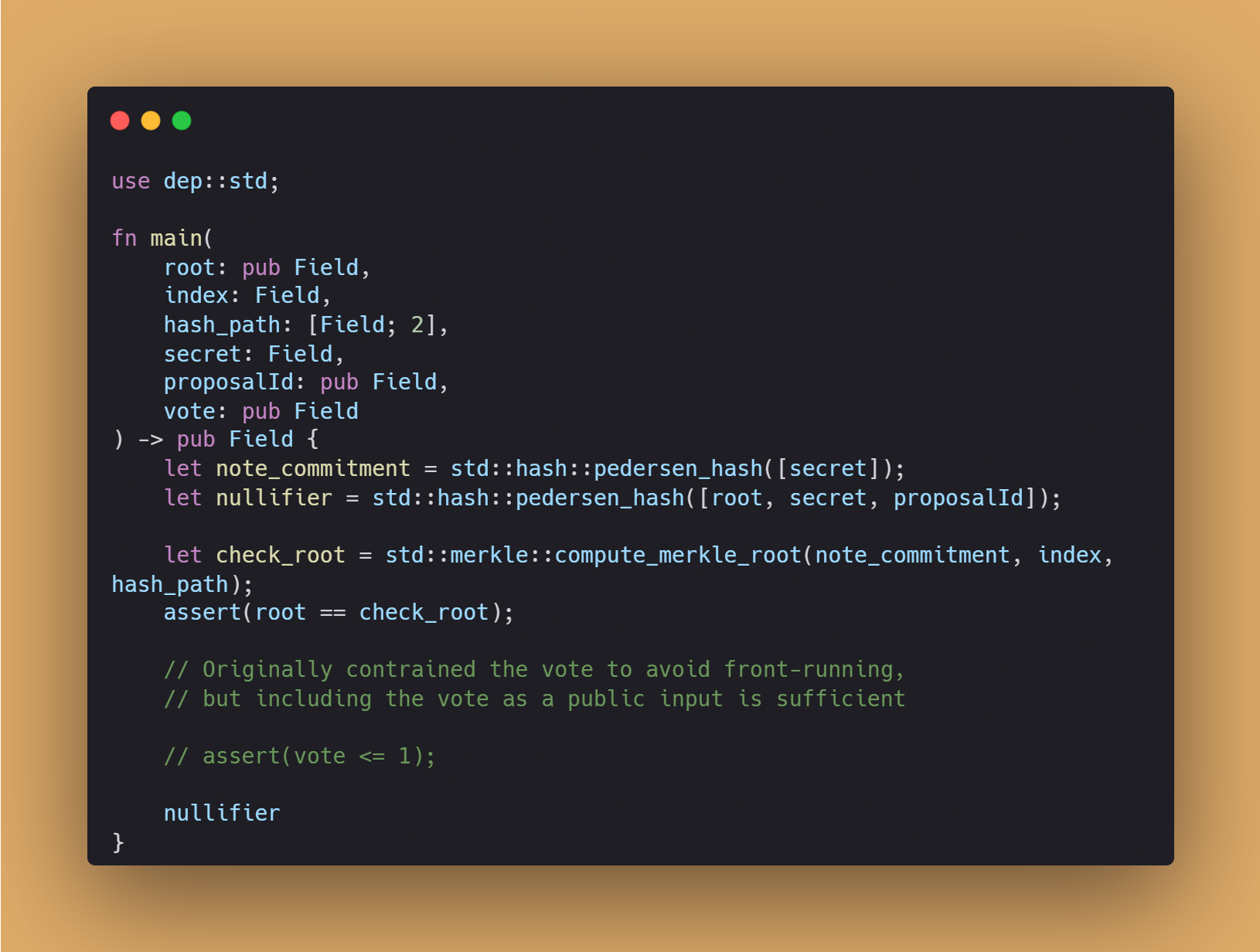
Let’s break down the steps of this program and explain why each one is important:

1. Program Inputs:

   • root: a public field representing the Merkle tree root that contains all participants’ “notes” (commitments).
   • index: a secret field indicating the location of a participant’s commitment within the Merkle tree.
   • hash_path: an array of two fields containing hashes to compute the path in the Merkle tree to the root.
   • secret: a secret field used to create the vote commitment.
   • proposalId: a public field, the identifier of the proposal being voted on.
   • vote: a public field, the value of the vote (for example, “for” or “against”).

2. Hashing of the Commitment and Nullifier:

   • note_commitment: created by hashing the secret. This serves as the participant’s commitment, ensuring anonymity.
   • nullifier: calculated as a hash of the tree root, secret, and proposal identifier. The nullifier is used to prevent reuse of the vote (double voting).

3. Verification of the Correct Position of the Commitment in the Merkle Tree:

   • check_root: calculated from the commitment, index, and hashing path to verify that the commitment is in the Merkle tree with the given root. This confirms that the participant indeed has the right to vote.

4. Assertion of Correct Root (assert):

   • assert(root == check_root): asserts that the calculated tree root matches the provided root. This ensures that the vote is counted in the current Merkle tree.

5. Program Output:

   • The program returns nullifier, which is used to register the fact of voting without revealing who voted or how.

This system ensures anonymity and transparency in voting, prevents the possibility of altering a vote after it is cast, and eliminates duplicate votes. Using public fields for vote and proposalId allows everyone to verify that a vote was cast for a specific proposal without revealing the identity of the voter.

Now, let’s take a look at the implementation of the same logic in Circom:

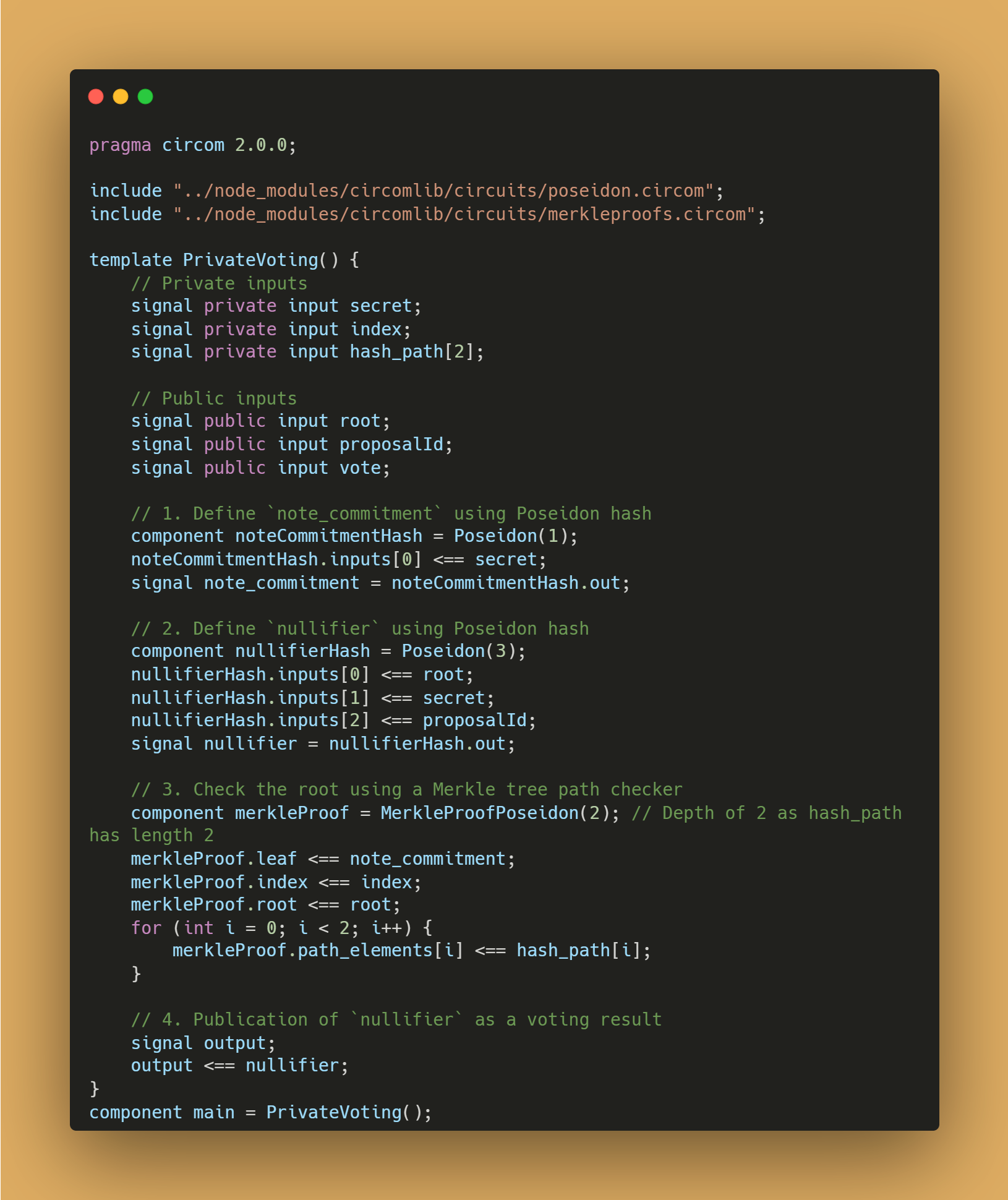
Here, the process is divided into the same logical steps, but there are significant differences from the first implementation. What are these differences?

Here are the main points to consider when comparing the Noir implementation to the Circom implementation:

1. Syntactic Clarity and Simplicity

Noir-lang offers a higher level of abstraction with syntax reminiscent of traditional programming languages (like Rust). This can make it easier for developers who are not specialists in cryptography to understand and develop. The code in Noir looks cleaner and easier to understand:

• The use of standard functions such as std::hash::pedersen_hash and std::merkle::compute_merkle_root makes the Noir code more readable and easier to analyze.
• Circom, on the other hand, requires more detailed setup and use of components, which can complicate the code and its maintenance.

2. Management of Components and Modularity

Noir-lang provides good modularity and ease of integration with other libraries and services thanks to its structured approach to modules and namespaces:

• Noir has a clear separation of public and private inputs, as well as the use of pub to explicitly denote public arguments, which enhances the clarity of expected inputs.

3. Built-in Functionality and Libraries

Circom requires the inclusion of external libraries for hashing and proof verification (like circomlib), whereas Noir can use standard libraries, simplifying dependency management and updates:

• In Noir, functionality such as hashing and calculations for Merkle trees are presented as built-in functions, which reduces the likelihood of errors due to incorrect use of libraries or components.

4. Optimization and Performance

Performance and compilation optimization can vary depending on the specific use of Noir and Circom, where each is optimized for its specific use cases:

• Noir may offer more optimized execution due to higher-level optimizations and abstractions, while Circom may require more careful manual optimization.

Conclusion

So, what conclusions can we draw?

• Noir is truly a unique language for writing circuits, offering developers a host of unique features.
• Noir allows for a significant reduction in the number of constraints in a circuit, which can greatly reduce the time it takes to generate a ZK proof.
• Noir is still evolving and can be a bit raw in places, but it has great potential to become the leading DSL in the development of ZK programs.
• Noir is significantly more convenient in terms of the available development tools and is actively striving to create its own ecosystem of tools that will allow for a full CI/CD cycle without the need for external solutions.

References

Aztec & Noir DSL

• [Link] - [#report] - “2023 Crypto Developer Report”
• [Link] - [#research] - “Aztec: Ethereum’s Privacy-focused ZK-rollup”
• [Link] - [#research] - “Aztec’s ZK-ZK-Rollup, looking behind the cryptocurtain”
• [Link] - [#research] - “Introducing Noir: The Universal Language of Zero-Knowledge”
• [Link] - [#documentation] - “The Noir Language”
• [Link] - [#documentation] - “Noir Playground”

Noir in practise

• [Link] - [#repository] - @AztecProtocol/aztec-packages/noir
• [Link] - [#repository] - @AztecProtocol/aztec-starter
• [Link] - [#repository] - @AztecProtocol/awesome-aztec
• [Link] - [#repository] - @noir-lang/noir-examples
• [Link] - [#repository] - @noir-lang/awesome-noir
• [Link] - [#repository] - @noir-lang/noir-starter
• [Link] - [#repository] - @noir-lang/noir